三角形の平等の兆し

2つのセグメントが等しいと誰もが知っていますそれらの長さは一致する。円の半径が等しい場合、円は等しいと見なすことができます。そして、三角形の平等の兆候は何ですか？中学校の7年生：幾何学の教訓では、生徒は、平等がそれらを含む三角形に等しいと考えることができる要素があることを知ります。問題を解決するのに非常に便利です。

三角形の平等の最初の符号

対応する平等の条件の遵守三角形および他の三角形にそれらの間に封入されている角度の両側で囲まれて二辺と角その間は、これらの三角形は同じであることを示唆しています。

証明。

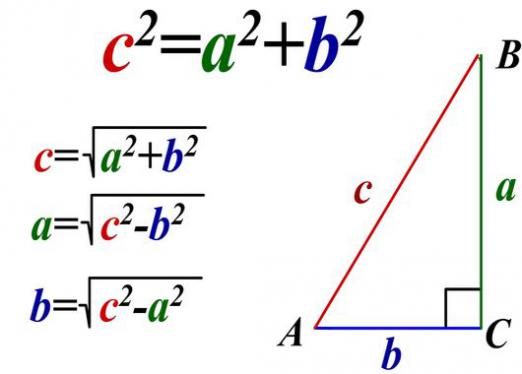
△AB = A1B1、BC = B1C1である△ABCと△A1B1C1を考えると、

∠ABCは∠A1B1C1と等しく、

∠A1B1C1と∠ABCとが一致するように、ΔA1B1C1をΔABCに重ね合わせることができる。この場合、すべての頂点が一致するため、三角形は完全に一致します。

（必要であれば、三角形A1B1C1は、等号「逆三角形」、すなわちA1B1C1と対称な三角形で置き換えることができます）。

三角形の平等の2番目の符号

一方の側と2つのコーナーそれらに隣接する三角形は、それぞれ別の三角形に隣接する辺および2つの角度に等しい場合、そのような三角形は等しいとみなされる。

証明。

△ABC、△A1B1C1の場合、以下の等式が成立する

AB = A1B1、

∠BAC=∠B1A1C1、

∠ABC=∠A1B1C1。

我々は三角形A1B1C1とABCをお互いに重ね合わせる等しい辺AB、A1B1とそれらに隣接する角度とが一致するようにする。前の例と同様に、必要に応じて、三角形A1B1C1を「回して戻す」ことができます。三角形は一致するため、等価とみなすことができます。

三角形の平等の3番目の記号

1つの三角形の3辺が別の三角形の3辺すべてにそれぞれ等しいとすると、そのような三角形は等しいとみなされる。証明。

△ABCと△A1B1C1については、A1B1 = AB B1C1 = BC C1A1 = CA辺A1B1が辺ABと一致し、頂点B1とB、A1とAが一致するように三角形A1B1C1を移動する。中心Aと半径ACの円と、中心Bと半径BCの2番目の円をとります。これらの円は、点ABと点Cと点C2とで対称な2点で交差する。したがって、三角形A1B1C1の転送後のC1は、点CまたはC2のいずれかと一致しなければならない。いずれにせよ、三角形△ABC =△ABC2が等しいので、△AB =△A1B1C1であることを意味する（事実、これらの三角形は線分ABに関して対称である）。

長方形の三角形の等号の記号

長方形の三角形では、脚の間の角度は直線であるため、任意の長方形の三角形にはすでに等しい角度があります。したがって、以下の発言が有効です。

長方形の三角形は、一方の脚が他方の脚と等しい場合は等しくなります。
三角形の対応する等辺線の条件とこれらの三角形の脚の1つが満たされている場合、長方形の三角形は等しくなります。

三角形の等価性を表す第2の基準から除外すると、脚部に隣接する直線角に関する条件（三角形の直角が等しくなる）は、以下のようになります。

そのような三角形は等しいが、cathet1つの長方形の三角形のそれぞれに隣接する鋭角は、別の長方形の三角形の脚と鋭角に等しい。

三角形の内角の和は常に180°であり、直角三角形の1つの角度は直線です。したがって、2つの長方形の三角形の鋭角が等しい場合、残りの角度は等しい。通常の非長方形の三角形の場合、等号を求めるには、それに対応する1つの辺と2つの隅がそれぞれ等しいことを知るだけで十分です。直角三角形では、1つの鋭角と斜辺のみが、図の平等を決定するために考慮され得る。