どのように二等辺三角形の角度を見つけるのですか?

二等辺三角形は3つの角度と3つの辺を持つ最も単純なポリゴン。あなたが二等辺三角形の角度を見つける方法を理解する前に、この幾何学的図形の特性を知る必要があります。
二等辺三角形のプロパティ
二等辺三角形のプロパティを考えてみましょう。
- 二等辺三角形では、両辺は等しい。第三者が基本です。
- このような三角形の底辺の角度は等しい。
- 幾何学図形の角から反対側に引かれた二等分線、中央値および高さも等しい。
- 二等辺三角形の頂点から底辺までの二等分線、中央値および高さが一致する。
- あなたが二等辺三角形の中に円を刻印し、そのような図の周りにそれを記述すると、それらの中心は同じ行に置かれます。
- ベースのコーナーは鋭くしかできません。
したがって、三角形内で2つの角度が等しく、その高さが中央値と二等分線と一致する場合、それは二等辺三角形です。これは二等辺三角形の主な記号です。
今、角度を見つける方法を検討してください二等辺三角形。そのような三角形も長方形である場合、その角度のうちの2つを見つけることは困難ではないので、それらは常に45度に等しく、これは二等辺三角形の特性および符号に従う。
- 角度の1つを知っていれば、いつでも計算することができます必要です。例えば、底辺の角度を文字αで表し、図の頂点の角度を文字βで表します。従って、角度αは、(π-β)/ 2に等しくなり、ここでπは定数である。
- 角度はアークサインから計算することもできます。 角度α= arcsin(a / 2R)、角度β= arcsin(b / 2R)ここで、aとbは三角形の辺であり、半径rの三角形の周りに円を描く必要があります。
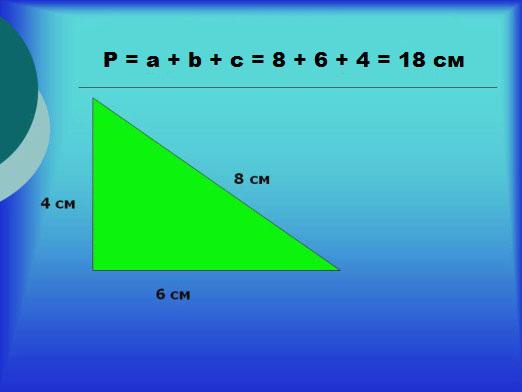
問題の解決の例
その底辺の角度が底辺の反対の角度よりも15度大きいことが分かっている場合は、二等辺三角形の角度を見つける必要があります。
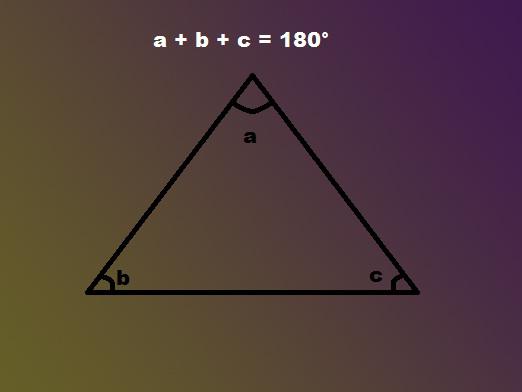
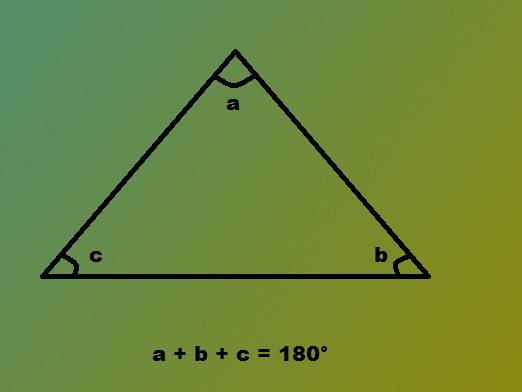
解決策:反対の角度βを指定すると、底面の角度はβ+ 15になります。三角形の合計は常に180度なので、次のようになります。
β+ 2×(β+ 15)= 180;
β+2β+ 30 = 180;
3β= 180-30;
3β= 150;
β= 50
したがって、底面の角度は50度です。他の2つの角度はそれぞれ65度に等しい。今、あなたは二等辺三角形の角度を見つける方法の規則を知っています。すべての計算であなたに幸運を祈っています!