周辺とは何ですか？

境界線 - 幾何学的用語の数学的、より正確には、主に図形の辺を計算するために使用されます。

私たちの記事では、基本的な幾何学的図形の例を使って、周囲が何であり、それがどのように測定されるかを学習します。

周辺の定義

周長は、すべての辺の長さの合計またはこれまたはその数字の円。周辺は、大きな文字「P」で示され、ミリメートル（mm）、センチメートル（cm）、メートル（m）などの様々な長さの単位で測定することができる。以下では、矩形の周長やその他の形状を調べる方法の例をいくつか示します。

周囲の測定

の周辺を知るために多角形では、定規が必要です。ルーラーでポリゴンのすべての辺を測定し、それらの図形を足し合わせると、境界線が何であるかが分かります。たとえば、13,14,15,17センチの辺を取得し、合計してP = 13 + 14 + 15 + 17 = 59センチになります。 。

複合体の周囲を知る必要がある場合数字（このような数字には線が不揃いの数字が含まれています）を入力すると、ロープや文字列が必要になります。これらの事柄の助けを借りて、図の正確な輪郭を記述することが必要であり、混乱しないようにするには、鉛筆でロープに印を付けることができます。または、それを切り取り、すべての部品を定規に取り付けることができます。したがって、ほぼすべての複雑な図形で周長が等しいことを知ることができます。

計算するための別のデバイスがあります複合形状の周囲：これは、曲率計（ローラー距離計）と呼ばれています。それを使用して、ローラーをシェイプ内の任意のポイントに設定し、ローラーでシェイプの輪郭を記述する必要があります。結果の数は、周長に等しくなります。他の幾何学的図形の周囲を見つけることについては、私たちの記事「周囲を見つける方法」から学ぶことができます。さて、さまざまな図形の周長を変更するいくつかの方法について詳しく説明します。

円、正方形、正三角形

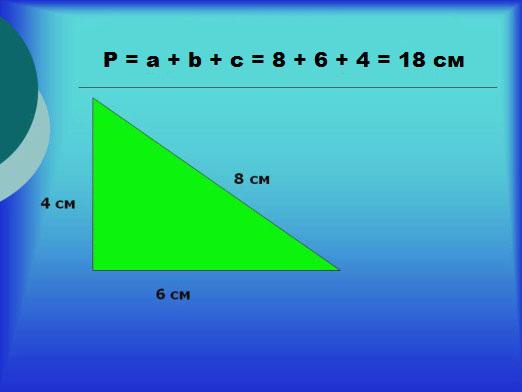
時には意味を決定するために周囲は、一部の図形、すべての関係者を置く必要はない、との乗算を使用することで十分です。例えば、辺の長さ値の正三角形の外周は、例えば、3を乗じなければならない見つけるかのパーティ - 次いで12 cmであり、P = 12×3 = 36 cmであり、全ての辺が同じ長さを有しているからです。あなたが三角形の周囲は何私達の記事を読むことによって学ぶことができます三角形に関するその他の興味深い情報。

周辺を見つける方法を見てみましょう円。それは非常に簡単です：周りを決定するだけで、半径rに数π3,14を掛けて2を足して（P = L = 2ππr）これを行うことができます。

もっと簡単な問題はこのような図形の周囲の定義は四角形です。これを行うには、正方形の1辺の長さを知っていれば十分です。その後、この値に4を掛けます。結果は必要な数になります。また、正方形の周囲を見つける方法の記事を読むことをお勧めします。