どのように直角三角形の側面を見つけるのですか?

幾何学は学校で最も複雑な科学の1つですプログラム。恐らく幾何学的問題の解を探している人にとっては最も難しいでしょう。この場合、最も正しいアプローチは、明確に計画されたアクションアルゴリズムです。つまり、式と定理の知識です。直角三角形の未知の部分の探索に関連する問題を解決するには、初期条件とピタゴラス定理を正しく使用することが重要です。さらに、直角三角形のプロパティに関する知識は重要です。このシリーズの問題の最も一般的な条件の例は、この記事で見つけることができます。
直角三角の辺を見てみましょう
周知のように、長方形の側面三角形はカタレまたは斜辺にすることができます。特定の条件を知っていれば、cathetと斜辺の両方を計算することができます。それによって、直角三角形の側面を見つける方法という主な質問に答えることができます。我々は、これらの条件および対応する解決策を検討する。
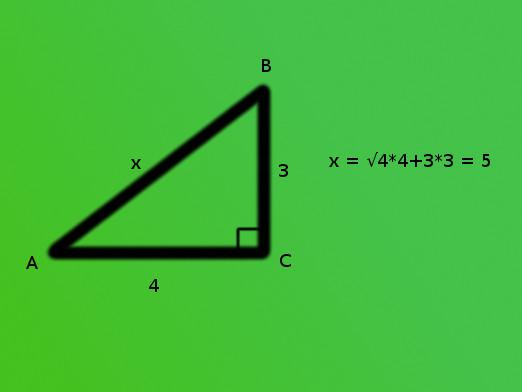
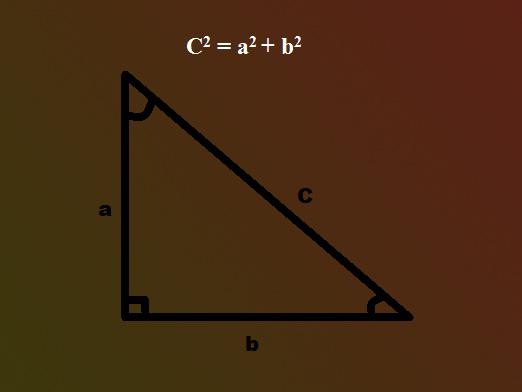
- 条件:両脚の長さは既知である。 斜辺はピタゴラスの定理を使って計算できます。この定理が何であるかを忘れてしまった人には、斜辺の四角形は脚の四角形の合計に等しいことを思い出してください。その知識を与えられた。 FB2 = BK2 + KF2ここで、FBは斜辺であり、BKとKFは足である。斜辺の長さを検索するときは、脚のサイズのそれぞれを交互に揃える必要があります。その後、結果の数値を加算し、結果から平方根を計算します。
- コンディション: 知られているのはカタレとそれに対する角度です。この角度は、斜辺とそれが取り付けられている脚によって形成される。既知の角度を記号aで表す。直角三角形の性質に従って、以下のように応答を書く:FB = BK * cos(a)
- コンディション: 知られているのはカテーテル(KF)であり、同じ角度αであり、これは今度は脚の反対側の位置にある。この場合の斜辺の検索では、直角三角形のプロパティは、脚の長さと斜辺の長さの比が脚の反対のsin角に等しいと言って、私たちを助けます。このように書く:FB = KF * sin(a)。
- 条件:既知の斜辺。 斜辺がACの直角三角形ABCを取る。点Aの頂点をLaとする角度cと、点Bの頂点をなす角度をLbとする必要がある。次に、脚ABとBCの長さを見つける必要があります。
- コンディション: 直角三角形のカテーテルが知られている。 BCはbと等しいと仮定することができる。この場合、私たちが知っているピタゴラスの定理(a ^ 2 + b ^ 2 = c ^ 2)を使用します。この方程式から、必要なcatet | AB | = a =√(c ^ 2 - b ^ 2)。
あなたが見ることができるように、ピタゴラスの定理を知っていれば、ジオメトリでこれらの一見困難な作業を行い、直角三角形の側面を簡単に見つける方法を個別に理解することができます。あなたが知らないなら、あなたはピタゴラスの定理を使う方法を知っています。あなたは既製の公式を使うことができます。