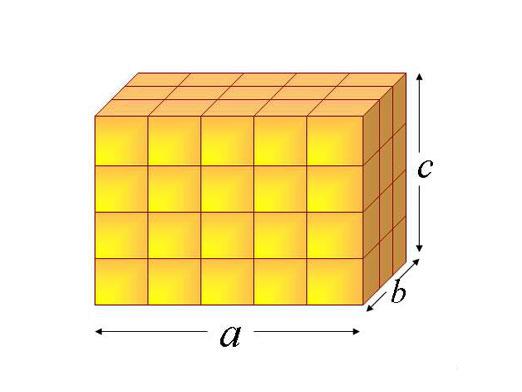
どのように平行六面体の領域を見つけるには？

幾何学図形では、平行六面体は6つの顔 - 4つの基本と2つの脚（定義上、すべて平行四辺形です）。 6つがすべて矩形であれば、平行六面体は直線になります。反対側の辺は等しく、平行です。平行六面体の4つの対角線は1点に収束し、2つに分かれている。

エリアの検索方法を知るには基底と辺の長さを決定しながら、最初にすべての基底（文字-aで示される）、その外側（文字-bで示される）の面積を計算する必要があります。

最初に、平行四辺形（文字-hで示される）、次に平行六面体の端（文字-Hで示される）の高さを描画します。または、辺の長さ（a、b、c）を通して。

塩基の総面積は、S = 2a * hまたはS = 2ac

側面は矩形であるため、S = 2a * H、S = 2b * h、S = 2a * b、S = 2b * c

そこで、私たちはそのエリアを見つける方法を考え出したS = 2ah + 2aH + 2bH = 2（ah + aH + bH）またはS = 2（Sa + Sb + Sc）= 2（ab + bc + ac）、すなわち面積の2倍の合計平行六面体の面。

側面が向いている場合があります平行四辺形はその底辺に対して任意の角度にあり、平行六面体は傾いている。次に、その高さを知って、その側面の面積が計算される。この場合、基底の面積は同じように計算されます。

複雑ではありません。