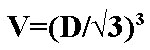どのようにして立方体の表面積を見つけるか?

キューブは、正方形の3次元バージョンです。 キューブのエッジの長さ(a)を知ると、表面積(S)を決定する最も一般的な公式を使用することができる。正方形の面積が立てられた正方形の長さに対応し、立方体が6であるという事実から進んで、S = 6・a²を得る。この数式は、立方体の全表面の面積を決定します。
立方体の面積を求める方法
- キューブの辺で囲まれた空間の体積(V)が与えられ、エッジの長さが未知である場合、領域(S)はこのように定義される。
唯一の既知の図形サイズ、第3の辺の隆起した辺の長さである場合、キューブの各面の辺の長さ寸法は、既存のパラメータから立方根を抽出することによって決定される。立方体の表面積の公式は次のとおりです。S = 6⋅(³√V)²。
- 六面体の対角長(L)が与えられると、1つの顔の長さを簡単に計算することができ、それと共に図形の面積も計算できます。対角線は以下のように定義される:L / v3。したがって、立方体の面積は次のように計算されます。S = 6⋅(L /√3)²= 2ÂL²。これは計算に非常に便利です。
- 指定したときにキューブの表面積を見つける方法六面体の周りに記述されている球の半径(R)?単純に! S = 8・R2 = 2・(2・R)²の式を適用するだけでよい。これは、キューブの対角線が球の直径パラメータに対応するという事実のために可能である。
- 六面体に内接する円の半径を知ると、立方体の表面積の公式は次のように書かれる:S = 24÷r²。
立方体の表面積
S = s1 + s2 + s3 + s4であり、これらの用語は、平行六面体の側面を形成する4つの平行四辺形の領域をそれぞれ表す。
立方体の外面の面積の公式は、基底Pと高さhの既知の周囲で、直方体が与えられれば、S = P・hと表すことができる。
計算を長方形で行う必要がある場合(すべての面が長方形である)、基底(dとc)の辺の長さが既知であるとき、kが図の側端であるとき、立方体の側面の面積はS = 2・k・(d + c)と定義される。