分数を見つけるには?
数学は科学の女王です。彼女の偉大さは無限ですが、彼女の力は素晴らしいです。他のすべての科学は数学的な結果に依存しています。それが物理学、化学、生物学、さらには文学であろうと。
家は煉瓦でできているので、各作業には小さなサブタスクがあります。小さく解くことを学ぶことによって、より複雑な問題を解決する方法を学ぶことができます。
今日、分数を見つける方法を分析します。 古代ギリシアでは、ギリシャ人が長さという概念を導入した後、分数の概念が整数に相当した。次に、長さの一部、例えば半分、長さの3分の1を表現する概念が必要でした。そこで、端数の概念が現れました。
有理数Qの集合は、m / nの形式で表される数の集合であり、m、nは整数である。数m / nは通常分数と呼ばれ、mは分子、nは分母、n≠0である。
n =〖10〗^ k、k = 1,2、...ならば、そのような小数は小数と呼ばれ、カンマがk-1の後の0の数と共に0,0..0mと書かれる。
数が1以外の他の除数を持つ場合、その数はコンポジットと呼ばれます。
基本操作
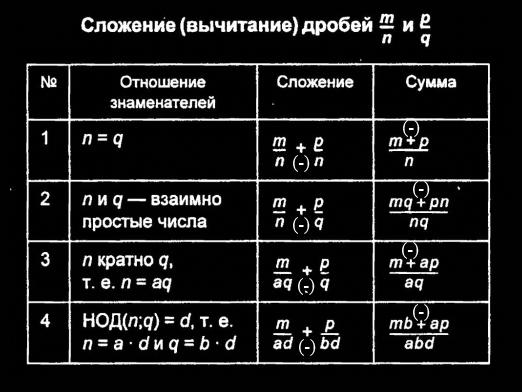
分数は、加算、減算、乗算、除算、または乗算することができます。これらの操作は基本的なものです。例では、
私たちは、これらの操作や他の操作がどのくらい正確に実行されるかを例で示しながら、単純なものから複雑なものへと移行します。
分数を減らす方法
これを行うには、分子と分母が複合因子である場合は、素因数で分子と分母を拡張する必要があります。さらに、これらの単純な要素が一致した場合は、それらを削除します。
素因数がない場合、その割合は既約と呼ばれます。たとえば、85/65 =(17 * 5)/(13 * 5)= 17/13
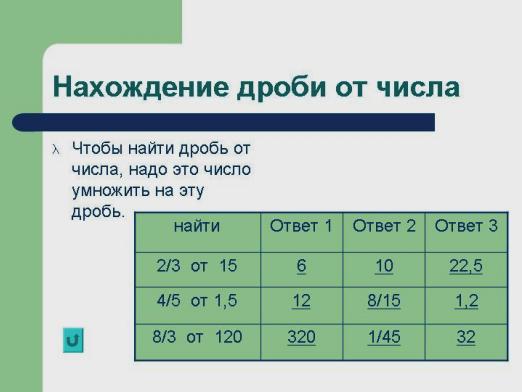
数から分数を見つける方法
数字を一定の長さにします。端数は基本的にこの長さの一部です。そのため、整数部分を見つけるには、端数に数値を掛けます。例えば、27の2/3 = 27×2/3 = 27/3×2 = 18
分数から分数を見つける方法
実際、これは単純な乗算処理であり、小数部を見つけるには2つの小数部を掛けるだけです。たとえば、2/3および13/17:2/3 * 13/17 = 26/51
フラクションの分裂
分数a / b、c / dを分割するとき、除数c / dはd / cとして表され、乗算されて切り取られます。例えば、27/17→9/34 = 27/17 * 34/9 = 2 * 3 = 6。
複雑な問題を解決する際には、例には解法アルゴリズムが必要です。分数の変更で除算を乗算に変更する必要がある場合もありますが、同じ数で乗除算を行うことは可能です。そのような単純な指示は、例を解決するのに役立ちます。
例として、古典的なテキストを取るタスク。 150トンの燃料油が2/3盗まれた倉庫から。盗難された部分は5/17と12/17の比率で部品に分配され、後者は処理のために輸送された。残りの燃料油は処理のために輸送された。どのくらいの燃料油がリサイクルされていますか?
150×2/3×12/17 + 150×(1-2 / 3)= 150×41/51
分数の仕事は学校の算数の基礎です。彼らは本質的に複雑ではありませんが、勤勉で注意深いことが求められます。これらの条件が満たされれば、結果は長くかかることはありません。